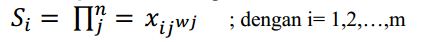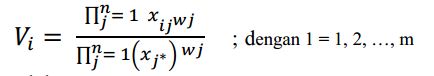Jawaban quis online Metode Topsis

Soal 
Suatu kelurahan mendapatkan Bantuan Langsung Tunai dari pemerintah untuk masing masing kepala keluarga dengan syarat ketentuan sebagai berikut :

C1 : Jumlah Tanggungan
C2 : Pendapatan Kepala Keluarga
C3 : Luas Bangunan Rumah
C4 : Memiliki KK


 Bobot W : [5,4,3,3]

Nama KK	C1	C2	C3	C4
Aldyan	2	2	3	1
Hendro	3	3	1	2
Joko	2	4	1	2
Doni	2	2	2	2
Dono	3	3	4	2
Kasino	2	2	2	2
Susento	1	4	5	1

Penyelesaian :

X1 =√2²+3²+2²+2²+3²+2²+4²=5,916         

R11= 2/5,916=0,3380                                  

R21= 3/5,916=0,5070

R31= 2/5,916= 0,3380

R41=2/5,916 = 0,3380

R51=3/5,916=0,5070

R61=2/5,916=0,3380

R71=1/5,916=0,6190

X2=√2²+3²+4²+2²+3²+2²+4²=7,874

R12= 2/7,874=0,2540                                  

R22= 3/7,874=0,3810

R32= 4/7,874=0,5080

R42=2/7,874=0,250

R52=3/7,874=0,3810

R62=2/7,874 =0,2540

R71=1/5,916=0,6190

X3=√3²+1²+1²+2²+4²+2²+5²= 7,745

R13= 3/7,745=0,3873                                  

R23= 1/7,745=0,1291

R33=1/7,745=0,1291

R43=2/7,745=0,2582

R53=4/7,745=0,5164

R63=2/7,745=0,2582

R73=1/5,916=0,6190

X4=√1²+2²+2²+2²+2²+2²+1²= 4,690

R14= 1/4,690=0,1232                                  

R24= 2/4,690=0,4264

R34= 2/4,690=0,4264

R44= 2/4,690=0,4264

R54=2/4,690=0,4264

R64=2/4,690=0,4264

R74=1/4,690=0,1232

Matrik Ternormalisasi terbobot Yij=W1.Rij

Y11= 5*0,3380 =1,96

Y21=5*0,5070 =2,535

Y31=5*0,3380 =1,96

Y41 =5*0,3380 =1,96

Y51= 5*0,5070 =2,535

Y61= 5*0,3380 =1,96

Y71=5*0,6190=3,095

Y12= 4*0,2540=1,016

Y22=4*0,3810=1,524

Y32=4*0,5080=2,032

Y42 =4*0,2540=1,016

Y52= 4*0,3810=1,524

Y62= 4*0,2540=1,016

Y72=4*0,5080=2,032

Y13= 3*0,3873=1,1619

Y23=3*0,1291=0,3873

Y33=3*0,1291=0,3873

Y43 =3*0,2582=0,7746

Y53= 3*0,5164 =1,5492

Y63= 3*0,2584=0,7746

Y73=3*0,6455=1,9365

Y14= 3*0,2132=0,6396

Y24=3*0,4264=1,2792

Y34=3*0,4264=1,2792

Y44 =3*0,4264=1,2792

Y54= 3*0,4264=1,2792

Y64= 3*0,4264=1,2792

Y74=3*0,2132=0,6396

Solusi Ideal Positif (A+)

Y1⁺ =Max (1,69 ; 2,535 ; 1,69 ; 2,535 ; 1,69 ; 3,095)=3,095

Y2⁺ =Min (1,061 ; 1,524 ; 2,032 ; 1,016 ; 1,524 ; 1,016 ; 2,032)= 1,016

Y3⁺ =Min (1,1619 ; 0,3893 ; 0,3873 ; 0,7746 ; 1,5492 ; 0,7746 ; 1,9365)= 0,3873

Y4⁺ =Max (0,6396 ; 1,2792 ; 1,2792 ; 1,2792 ; 1,2792 ; 1,2792 ; 0,6396) = 1,2792

Solusi Ideal Negatif (A-)

Y1^- =Min (1,69 ; 2,535 ; 1,69 ; 2,535 ; 1,69 ; 3,095)=1,69

Y2^- =Max (1,061 ; 1,524 ; 2,032 ; 1,016 ; 1,524 ; 1,016 ; 2,032)= 2,032

Y3^- =Max (1,1619 ; 0,3893 ; 0,3873 ; 0,7746 ; 1,5492 ; 0,7746 ; 1,9365)= 1,9365

Y4^- =Min (0,6396 ; 1,2792 ; 1,2792 ; 1,2792 ; 1,2792 ; 1,2792 ; 0,6396) = 0,6396

Solusi Jarak Antara Nilai setiap Alternatif (Di+)

D1⁺ =√(1,69-3,095)²+(1,016-1,016)²+(1,1619-0,3873)²+(0,6396-1,2792)² =2,983

D2⁺ =√(2,535-3,095)²+(1,524-1,016)²+(0,3873-0,3873)²+(1,279-1,2792)² =0,5716

D3⁺ =√(1,69-3,095)²+(2,032-1,016)²+(0,3873-0,3873)²+(1,2792-1,2792)² =3,004

D4⁺ =√(1,69-3,095)²+(1,016-1,016)²+(0,7746-0,3873)²+(1,2792-1,2792)² = 2,124

D5⁺ =√(2,535-3,095)²+(1,524-1,016)²+(1,5492-0,3873)²+(1,2792-1,2792)² =1,9216

D6⁺ =√(1,69-3,095)²+(1,016-1,016)²+(0,7746-0,3873)²+(1,2792-1,2792)² =2,124

D7⁺ =√(3,095-3,095)²+(2,032-1,016)²+(1,9365-0,3873)²+(0,6396-1,2792)² =3,8412

Solusi Jarak Antara Nilai setiap Alternatif (Di^-)

D1^- =√(1,69-1,69)²+(1,016-2,032)²+(1,1619-1,9365)²+(0,6396-0,6396)² =1,6322

D2^- =√(2,535-1,69)²+(1,524-2,032)²+(0,3873-1,9365)²+(1,2792-0,6396)² = 3,803

D3^-  =√(1,69-1,69)²+(2,032-2,032)²+(0,3873-1,9365)²+(1,2792-0,6396)² = 2,809

D4^-  =√(1,69-1,69)²+(1,016-2,032)²+(0,7746-1,9365)²+(1,2792-0,6396)² = 2,013

D5^-  =√(2,535-1,69)²+(1,524-2,032)²+(1,5492-1,9365)²+(1,2792-0,6396)² =1,531

D6^- =√(1,69-1,69)²+(1,016-2,032)²+(0,7746-1,9365)²+(1,2792-0,6396)² =2,7912

D7^- =√(3,095-1,69)²+(2,032-2,032)²+(1,9365-1,9365)²+(0,6396-0,6396)² =1,9740

Solusi Preperensi (Vi)

V1= 1,6322 / 2,983+1,6322 = 0,3536

V2= 3,803/ 0,5716+3,803= 0,8693

V3= 2,809/ 3,004+2,809 = 0,4832

V4= 2,013/ 2,124+2,013 = 0,4865

V5= 1,531/ 1,9216+1,531= 0,4434

V6= 2,7912/ 2,124+2,7912 =0,5576

V7= 1,9740/ 3,8412+1,9740 = 0,3394

Metode Weighted Product WP dalam Sistem Pendukung Keputusan (SPK)

Metode Weighted Product WP dalam Sistem Pendukung Keputusan (SPK)

Metode Weight Product (WP)
Metode  WP  mengunakan perkalian untuk menghubungkan rating atribut, di mana rating setiap atribut harus dipangkatkan dulu dengan bobot atribut yang bersangkutan.
Proses ini Ai diberikan sebagai berikut :

Dimana  ∑wj =  1.  wj  adalah  pangkat  bernilai  positif  untuk  atribut  keuntungan,  dan bernilai negatif untuk atribut biaya.
Preferensi relatif dari setiap alternatif, diberikan sebagai:

Contoh kasus :
Misalkan nilai setiap alternatif pada setiap atribut diberikan berdasarkan data riil yang ada seperti pada Tabel 2.1, perlu diidentifikasi terlebih dahulu jenis kriterianya, apakah termasuk kriteria keuntungan atau kriteria biaya.

Rating kecocokan dari setiap alternatif pada setiap kriteria
(Kusumadewi, Hartati, Harjoko, dan Wardoyo, 2006: 78)

Kriteria C2 (kepadatan penduduk di sekitar lokasi) dan C4 (jarak dengan gudang  yang sudah  ada)  adalah  criteria  keuntungan.  Sedangkan  kriteria  C1(jarak  dengan  pasar terdekat), C3 (jarak dari pabrik), dan C5 (harga tanah untuk lokasi) adalah kriteria biaya.Permasalahan kasus di atasakan di selesaikan dengan menggunakan metode  Weighted Product (WP). Sebelumnya akan dilakukan perbaikan bobot terlebih dahulu. Bobot awal W = (5, 3, 4, 4, 2), akan diperbaiki sehingga total bobot ∑Wj = 1, dengan cara :

Kemudian vektor S dihitung berdasarkan persamaan  dengan i = 1, 2, … ,m sebagai berikut :

Nilai  vektor  yang  akan  digunakan  untuk  perankingan  dapat  dihitung  berdasarkan persamaan

Nilai terbesar ada pada V2  sehingga alternatif A2 adalah alternatif yang terpilih sebagai alternatif  terbaik.  Dengan  kata  lain,  alternatif  A2 akan  terpilih  sebagai  lokasi  untuk mendirikan gudang baru. ( Kusumadewi, Hartati, Harjoko, dan Wardoyo, 2006: 79 )

sumber : undip.ac.id